..:: LOJİK DEVRE TASARIMI ::..
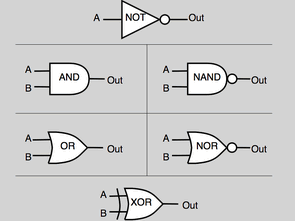
Lojik kapılar kullanılarak bir çok lojik devre hazırlanabilir. Bu devreler dijital elektroniğin temel taşlarını oluşturmaktadır.
Lojik Kapılarla Yapılan Devre Örnekleri
2 Girişli AND Kapısı Kullanılarak 4 Girişli AND Kapısı Yapılması:
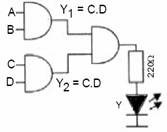
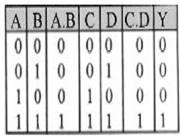
Görüldüğü üzere yukarıdaki devrede ledin ışık verebilmesi için tüm lojik girişlerden “lojik 1” sinyali almamız gerekir.
2 Girişli OR Kapısı ve NOT Kapısı Kullanarak NOR Kapısı Yapılması:
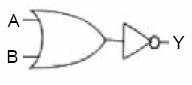

OR kapısının çıkışının, NOT kapısı tarafından değili alınır. Bu sayede NOR kapısı elde etmiş oluruz.
2 Girişli NOR kapılarından 3 Girişli NOR Kapısı Yapılması:
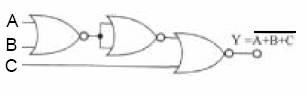
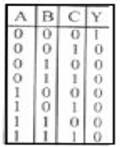 Yandaki doğruluk tablosundan da anlaşılabileceği üzere 3 adet 2 girişli NOR kapısı şekildeki gibi bağlanarak 3 girişli bir NOR kapısı elde edilmiştir.
Yandaki doğruluk tablosundan da anlaşılabileceği üzere 3 adet 2 girişli NOR kapısı şekildeki gibi bağlanarak 3 girişli bir NOR kapısı elde edilmiştir.
2 Girişli OR Kapıları Kullanılarak 4 Girişli OR Kapısı Yapılması:
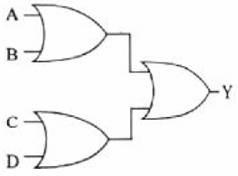
NAND ve NOT Kapıları Kullanılarak AND Kapısı Yapılması:
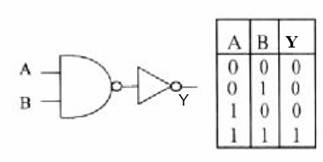
Boolean Denklemleri Kullanılarak Lojik Devre Çizilmesi
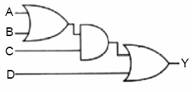
Örnek: Y = A + B.C denkleminin lojik kapılı devresini çiziniz.
Çözüm:
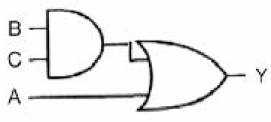
Örnek: Y = [(A + B).C] + D denkleminin lojik kapılı devresini çiziniz.
Çözüm:
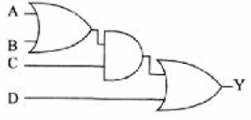
Örnek: ![]() denkleminin lojik kapılı devresini çiziniz.
denkleminin lojik kapılı devresini çiziniz.
Çözüm:
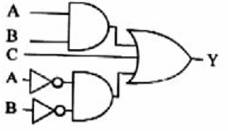
Örnek: ![]() denkleminin lojik kapılı devresini çiziniz.
denkleminin lojik kapılı devresini çiziniz.
Çözüm:
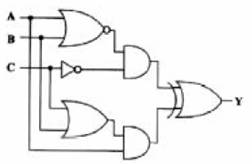
Örnek: ![]() denkleminin lojik kapılı devresini çiziniz.
denkleminin lojik kapılı devresini çiziniz.
Çözüm:
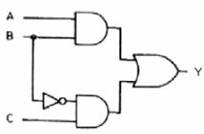
Örnek: ![]() denkleminin lojik kapılı devresini çiziniz.
denkleminin lojik kapılı devresini çiziniz.
Çözüm:
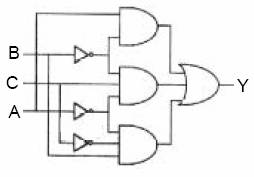
Örnek: ![]() denkleminin lojik kapılı devresini çiziniz.
denkleminin lojik kapılı devresini çiziniz.
Çözüm:
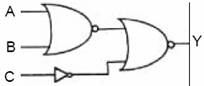
Lojik Devrelerden Yararlanarak Boolean Denklemlerinin Yazılması
Aşağıda verilen lojik devrelerin Boolean denklemlerini yazalım.
Örnek:
Çözüm:
![]()
Örnek:
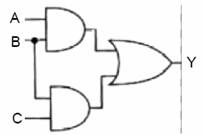
Çözüm:
![]()
Örnek:
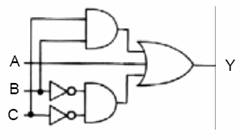
Çözüm:
![]()
Örnek:
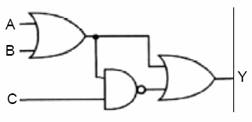
Çözüm:
![]()
Örnek:
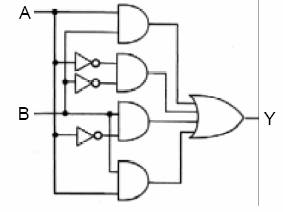
Çözüm:
![]()
NOT: Karmaşık yapılı lojik devrelerde NOT kapısının sembolü daire şeklinde ifade edilebilir.
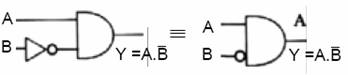
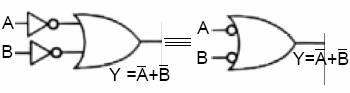
Lojik Kapılı Devrelerin Boolean Teoremleriyle Sadeleştirilmesi
Dijital devrelerin en az eleman kullanılarak yapılması istenir. Lojik kapılarla yapılan tasarımlar, Boolean teoremleri kullanılarak sadeleştirilebilir. Aşağıdaki örneklerle bu sadeleştirmeler daha net biçimde anlaşılabilir.
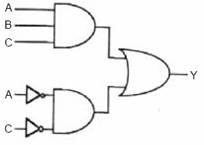
Örnek: ![]()
a. Lojik ifadenin sadeleşmemiş devresini çiziniz.
b. Lojik ifadeyi Boolean teoremlerini kullanarak sadeleştiriniz
c. Sadeleşmiş ifadenin lojik devresini çiziniz.
Çözüm:
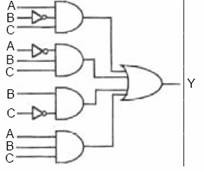
a.
b.
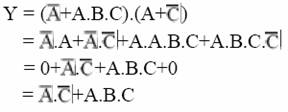
NOT: Boolean teoremleri gereğince yukarıdaki denkleme A.B.C eklenmesi sonucu değiştirmez. Bunun sebebi ise veya kapısına verdiğimiz girişin aynısından tekrar giriş vermemiz veya kapısının çıkışını değiştirmez.
c.
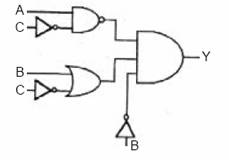
Örnek: ![]()
a. Lojik ifadenin sadeleşmemiş devresini çiziniz.
b. Lojik ifadeyi Boolean teoremlerini kullanarak sadeleştiriniz
c. Sadeleşmiş ifadenin lojik devresini çiziniz.
Çözüm:
a.
b.
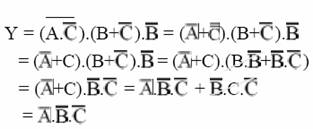
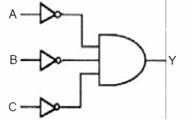
c.
NAND Kapısından Diğer Lojik Kapıların Eldesi
Lojik devreler yapılırken sadece NAND kapısı tüm işlemler için yeterli olmaktadır. Her kapının yapımında kullanabilen NAND kapısına bu özelliği dolayısıyla universal kapı da denilmektedir.
NAND Kapısından NOT Elde Edilmesi
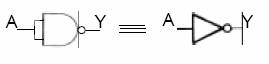
NAND Kapısından BUFFER Elde Edilmesi
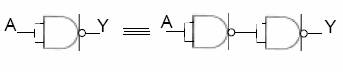
NAND Kapısından OR Elde Edilmesi
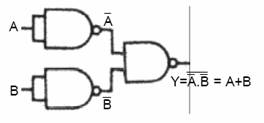
NAND Kapısından NOR Elde Edilmesi
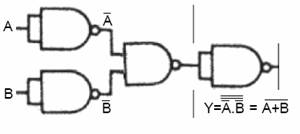
Lojik Kapıların NOR Kapısından Elde Edilmesi
NOR kapısından da diğer lojik kapıları elde edebiliriz.
NOR Kapısından NOT Kapısı Elde Edilmesi
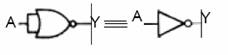
NOR Kapısından OR Kapısı Elde Edilmesi
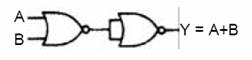
NOR Kapısından AND Kapısı Elde Edilmesi
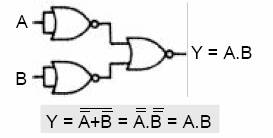
Özen ÖZKAYA
İTÜ OTOKON Eğitim Komitesi
Animasyonlar ile desteklenmiş İlgili bir yazı: AND-NAND OR-NOR XOR-XNOR
Yayım tarihi: 2013/08/17 Etiketler: itü lojik, lojik devre tasarımı, lojik devreler, lojik kapı devreleri, lojik kapılar, lojik uygulamalar, nand kapısı, not kapısı, or kapısı

İTÜ’de Bunlarımı Soruyorlar 🙂 Ben 11.Sınıfım Bunlardan Daha Zorlarını Yapıyoruz.
Sen itü’ye gel de görürsün 11. sınıf sorularını …
Liseliyle ne Alaka Deci;)Salla
aynen öyle bunları sorsalar aa gelir bütün dersler
Yarin sinav var cozelim bari ayip olmasin
Bi yapar mısın 4 senedir veremedim bu dersi bi çözüm
Allah rızası için soruları
https://ibb.co/55FtnDX
(A+B)(x)C
(x)= yuvarlak içinde çarpı
2. sorunu yapmam çünkü daha yeniyim