Teoriden Gerçeğe: Goertzel Algoritması (Vol. I)

Ülkemizde özellikle ‘kopyala-yapıştır programcılık’ mantığıyla çalışan kişi sayısının artmasından bıkan biri olarak, özellikle bir işin nasıl olması gerektiğine kendimce bir yanıt vermeyi amaçladığım bu yazı dizimde, final döneminde rastladığım, kısa notlar ve örneklerle pekiştirdiğim Goertzel algoritmasına değineceğim.

Kısaca değinmek gerekirse, Dr. Gerald Goertzel’in 1958 yılında yayınladığı Goertzel algoritması sinyalin içerisindeki frekans bileşenlerini çözen dijital sinyal işleme tekniğidir. Temel FFT algoritması tanımlı bir bant aralığındaki frekans bileşenlerini bizlere sunarken Goertzel algoritması sadece belirlenen, spesifik frekans bileşenlerini bizlere sunmaktadır.

Algoritmanın matematiksel ifadesi aşağıdadır:

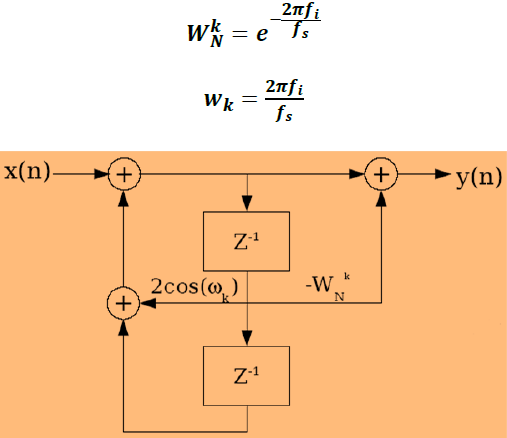
a) Örnekleme Oranı

Goertzel algoritmasında, aynen FFT’de olduğu gibi, örnekleme frekansı, belirlenmesi istenen frekansların en büyüğünün en az iki katı olmalıdır.

b) Blok Boyutu

Goertzel blok boyutu N aynı FFT’de olduğu gibi filtre sonucunda çıkacak frekans çözünürlüğüne etki eder. Blok boyutunu N ile temsil edersek frekans çözünürlüğü aralığı fs/N olacaktır. Örneğin örnekleme frekansı fs=8kHz, filtre uzunluğu N=100 seçilirse sonuçta çıkacak frekans çözünürlüğü 80Hz olacaktır.

Blok boyutunu büyük seçmek, özellikle düşük frekans bileşenlerinin daha iyi kararlılıkla belirlenmesine yol açsa da büyük seçilen blok boyutu Goertzel algoritması hesaplamasını bir o kadar uzatacaktır. Dolayısıyla blok boyutu seçiminde bu iki kriter göz önüne alınarak optimum seçimin yapılması gerekmektedir. Son olarak seçilecek olan N değeri, FFT’nin aksine, 2’nin katları olmak zorunda değildir.

c) Sabitler

Goertzel algoritmasını hesaplamadan önce Goertzel algoritmasının kullanacağı katsayıları hesaplamak işlemler sırasında algoritma çözümüne hız kazandıracaktır.

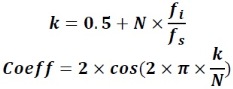
Yukarıdaki katsayılar her bir tespit edilecek frekans için ayrı ayrı bulunur. Yukarıdaki N sayısı blok boyutunu temsil etmektedir.

d) Temel Goertzel

Temel Goertzel algoritması DFT ve FFT’de olduğu gibi geriye sanal frekans bileşenlerini sunar. Genlik ve faz bilgileri geriye dönen bu sanal bileşenlerden yola çıkılarak hesaplanabilir.

Geortzel algoritması hesabında Q0, Q1 ve Q2’den oluşan 3 değişken sürekli hesaplanmak zorundadır.
Bu değişkenlerin başlangıç değerleri sıfır olmak koşuluyla Goertzel algoritması aşağıdaki gibi yazılabilir.

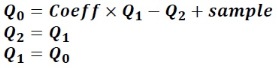
Yukarıdaki denklemler N kez tekrarlanır.
Daha sonra ortaya çıkan Q0, Q1 ve Q2 sayıları aşağıdaki denklemlerde kullanılır.

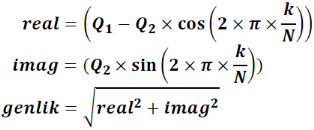
Yine bu denklemler belirlenecek frekans sayısı kadar tekrarlanarak her bir frekans için genlik değeri bulunmuş olur.

e) Optimize Edilmiş Goertzel

Optimize edilmiş Goertzel algoritması faz açıları yerine sadece genliklere odaklanır ve temel Goertzel algoritmasından daha az işlem yapılmasını sağlar.

Q0, Q1 ve Q2 katsayıları hesaplandıktan sonra temel Goertzel’den farklı olarak yapılması gereken tek işlem;

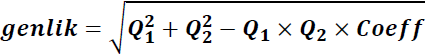
Mikrodenetleyiciler ile bu işlem yapılırken genliği büyük olan işleme alınacaksa karekök alma işlemine gerek yoktur. Dolayısıyla buradan denklem aşağıdaki forma dönüşür.

f) FFT ve Goertzel Algoritmasının Karşılaştırılması

Yüksek sayıda örnek için FFT her ne kadar avantajlı gözükse de Goertzel düşük sayıda frekansı çözümlemek için FFT’den daha hızlıdır. Genel anlamda N blok boyutu için FFT N(log2)N Goertzel (5/6)(log2)N kadar işlem yapmaktadır.

g) Matlab Uygulaması

Goertzel algoritması için her ne kadar Matlab kendi fonksiyonunu barındırsa da yukarıdaki denklemleri kullanarak yazdığımız .m kodlarını aşağıda görebilirsiniz. Aşağıdaki kodlardan da görülebileceği üzere DTMF keypad tuşlarından 3 örneklenmiştir.

% Yazar: Fırat DEVECİ
% Konu : Goertzel Algoritması

clear all;
Fs   = 4000;           % Örnekleme frekansı
n=0:1/Fs:0.1;           % Örnek
Goertzel_N=length(n);   % Goertzel örnek sayısı


freq=[697, 770, 852, 941, 1209, 1336, 1477, 1633];  % Bulmak istediğimiz frekans bileşenleri
Bins=length(freq);                                  % Kaç adet frekans bulacağımız bilgisi
samples=sin(2*pi*697*n)+sin(2*pi*1477*n);           % Örneklediğimiz sinyal
sound(samples);                                     % Ses çalınıyor

for i=1:Bins                            % Goertzel katsayıları hesaplanıyor
    k(i)=(0.5+(Goertzel_N*freq(i))/Fs);
    coeffs(i)=2*cos(2*pi*k(i)/Goertzel_N)
end

prev1=[zeros(Bins)];
prev2=[zeros(Bins)];

for i=1:Goertzel_N                      % Hangi frekansın baskın olduğu bulunuyor
    for j=1:Bins                        % Goertzel algoritması
        val=coeffs(j)*prev1(j)-prev2(j)+samples(i);
        prev2(j)=prev1(j);
        prev1(j)=val;
    end
end

for i=1:Bins                            % Genlikler bulunuyor
    magnitude(i)=sqrt((prev1(i)*prev1(i)+prev2(i)^2)-(coeffs(i)*prev1(i)*prev2(i)));
end

freq_indices = round(freq/Fs*Goertzel_N)+1;
dft_data = goertzel(samples,freq_indices);

subplot(3,1,1);
plot(n,samples);
title('Sinyal Şekli');
subplot(3,1,2);
stem(freq,abs(magnitude));              % Ekrana basılıyor
set(gca,'xtick',freq); 
xlabel('Hz');
ylabel('Magnitude');
title('Kendi Goertzel Algoritmamızın Yanıtı');
subplot(3,1,3);
stem(freq,abs(dft_data));
set(gca,'xtick',freq); 
xlabel('Hz');
ylabel('Magnitude');
title('Matlab Goertzel Algoritmasının Yanıtı');

Yukarıdaki kod işletildiğinde ekrana aşağıdaki şekil (üzerine tıklarsanız büyür) ortaya çıkmaktadır. Görüldüğü üzere kendi yazdığımız optimum Goertzel algoritması oldukça sağlıklı sonuç vermektedir.

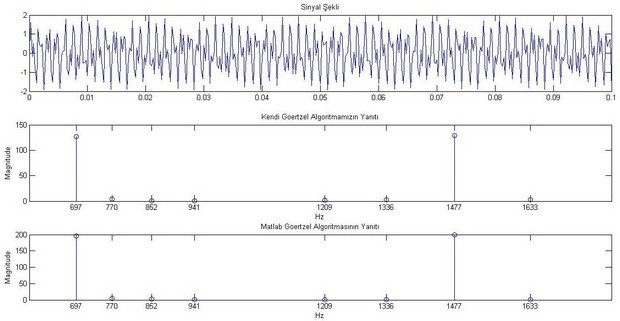
h) ANSI C Uygulaması

Yukarıda Matlab için yaptığımız uygulamayı ANSI C ortamına taşırsak aşağıdaki kod öbeğine ulaşmış oluruz.

/*
Yazar: Fırat DEVECİ
Konu : Goerzel Algoritması
*/

#include "stdio.h"
#include "stdlib.h"
#include "math.h"

#define Fs              4000            // Örnekleme frekansımız, izleyeceğimiz en yüksek frekans değerinin en az iki katı olmalı
#define BINS            8               // 8 temel frekans izlenecek
#define Pi              3.141592654     // Pi sayısı tanımlanıyor
#define GOERTZEL_N      128             // 128 örnek alınacak
#define Level_Segment   8

const int   freqs    [BINS] = {697, 770, 852, 941, 1209, 1336, 1477, 1633};
float       samples  [GOERTZEL_N];

float       coeffs   [BINS];
float       prev1    [BINS];
float       prev2    [BINS];
float       magnitude[BINS];
int         levels   [BINS];
float       n        [GOERTZEL_N];

unsigned char sample_counter    = 0;
unsigned char sample_complete   = 0;

// Goertzel için katsayılar hesaplanıyor

void coefficient(void)
{
    unsigned int k, i;
    for(i=0;i < BINS;i++)
    {
        k           =(unsigned int)(0.5 + (float)GOERTZEL_N * freqs[i] / Fs);
        coeffs[i]   = 2.0 * cos(2.0 * Pi * ((float)k/GOERTZEL_N));
    }

}

int goertzel(void)
{
    int big =0,
        i   =0;
    float val = 0,
          max = 0;

    // Geçici dizilerin içerisi temizleniyor
    for(i=0;i < BINS;i++)
    {
        prev2[i]=0;
        prev1[i]=0;
    }

    // GOERTZEL Algoritması işletiliyor
    for(sample_counter=0;sample_counter < GOERTZEL_N; sample_counter++)
    {
        for(i=0;i < BINS;i++)
        {
            val     = coeffs[i] * prev1[i] - prev2[i] + (float)samples[sample_counter];
            prev2[i]= prev1[i];
            prev1[i]= val;
        }
    }

    // Genlikler belirleniyor
    for(i=0;i < BINS;i++)
    {
        magnitude[i] = (prev1[i] * prev1[i]) + (prev2[i] * prev2[i]) - (coeffs[i] * prev1[i] * prev2[i]);
        if(magnitude[i] > max)
        {
            max=magnitude[i];
            big=i;
        }
    }

    for(i=0;i < BINS;i++)
    {
        levels[i]=(int)(Level_Segment*(float)(magnitude[i]/max));
    }

    return big;
}

int main()
{
    int i,buyuk;
    float a;
    coefficient();


    for(i=0;i < GOERTZEL_N;i++)
        samples[i]=sin(2*Pi*697*i/4000)+sin(2*Pi*1477*i/4000);

    buyuk=goertzel();

    printf("Yazar: Firat DEVECI\n");
    printf("Konu : Goertzel Algoritmasi\n\n");
    printf("En Buyuk Genlik: %d\n\n",buyuk);
    printf("Frekanslar      Katsayilar      Goertzel Sonucu\n");

    for(i=0;i < BINS;i++)
    {
        if(i==buyuk)
            printf("%d\tHz -    %f\t -  %d*\n",freqs[i],coeffs[i],levels[i]);
        else
            printf("%d\tHz -    %f\t -  %d\n",freqs[i],coeffs[i],levels[i]);

    }

        getch();
}

Yukarıdaki kodlar herhangi bir C (Code Blocks vb.) derleyicide derlendiğinde aşağıdaki çıktı ekranı ile karşılaşılır.

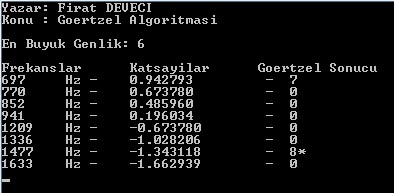
Sonuç

Goertzel algoritması yukarıdaki örneklerden de görüleceği üzere anlaşılması kolay, FFT'ye göre oldukça hızlı ve özellikle düşük güçteki mikrodenetleyiciler ile kolaylıkla kullanılabilecek yapıdadır. Özellikle DTMF kod çözümleme uygulamalarında tercih edilmesinin altında bu yatmaktadır.

Gelecek bölüm: Goertzel algoritmasının mikrodenetleyici ile gerçeklenmesi.