Smoothing Algorithms (Yumuşatma Algoritmaları)

Elektroniğin ve bir çok mikrodenetleyici uygulamanın geneli dış dünyadan ölçüm alıp, bunu işleme üzerinedir. Süreklilik arz eden gerçek dünyadan (buna analog dünya da denebilir) dijital yani örneklemeye dayalı dünyaya geçişte, iyi bir betimleme yaparken çeşitli sorunlarla karşılaşırız; çözünürlük, örnekleme süresi, gürültüler vb.

Çözünürlük ve örnekleme süresi gibi etmenler mikrodenetleyici seçiminde dikkate alınarak belirlenirler. Fakat gürültüler önceden tahmin edilemeyeceklerinden özellikle programcılar için büyük sorunlar doğurabilmektedir.

Simülasyon Dünyasından Gerçek Dünyaya

Mikrodenetleyicilerle ilk kez uygulama yapacak kişilerin klişe sorusudur; yaptığım ölçüm devresi simülasyon ortamında mükemmel çalışırken gerçekte çalışmıyor, nedeni nedir? Elbetteki simülasyon ortamında çalışan devre gerçek ortamda çalışırken sorunlarla karşılacaktır, çünkü simülasyon ortamında tüm elemanlar ideal, tüm zamanlar keskindir. Oluşan sinyal teorik olduğundan kesin ve nettir.

Gerçek ortamda ise şebeke, kullanıyorsak SMPS’ler, cihazımızın yanında çalışan büyük motorlar ve bir çok etmen sinyalimizi bozar, istemediğimiz ölçümler almamıza neden olurlar. Bu tür etkileri azaltmanın yegane yolu ise filtrelemedir.

Smoothing Filters

Yukarıda saydığımız etkileri yok etmenin en kolay yolunun filtre kullanmak olduğunu söylemiştik. Filtreleme’de uygulanan yöntem ise ölçülmek istenen sinyal dışındaki bileşenlerin bastırılmasına dayanmaktadır. Örneğin DC gerilim seviyesinde bir sinyal ölçecek ve şebekenin bu sinyali bozmasını istemiyorsak alçak geçiren bir filtre tasarlar, köşe frekansını ise 50Hz’den düşük noktada seçerek şebekenin ölçmek istediğimiz sinyale çok fazla müdahalede bulunmasını engelleriz. Bunun gibi ölçüm yapmak istediğimiz değerlere göre low, high, band pass gibi bir çok filtre kullanarak ölçümümüzü hatasız yapmaya çalışırız.

Filteleme yaparken ise önümüzde iki yol vardır; analog ve dijital filtreleme. Analog filtrelemede LCR ve bazı durumlarda opamp kullanılarak istenmeyen frekansların bastırılması sağlanır. Eleman değerlerinin sıcaklığa göre değişkenlik göstermesi, özellikle kapasitörün ESR direnç etkisi, ömrünün az olması gibi etmenlerden oldukça fazla sorunla baş etmemizi gerekmektedir. Sisteme artı bir maliyet yüklese de yüksek güçlerde analog filtrelemeden kurtulmak mümkün değildir.

Dijital filtreleme de ise özellikle günümüzde hızları artan mikrodenetleyiciler ve ADC’ler ile daha çok ön plana çıkmaktadırlar. Özellikle ses işlemlerinde çok kullanılan dijital filtreleme, zamanla değişkenlik göstermemesi, sisteme artı bir maliyet getirmemesi gibi avantajlara sahipse de işlem gücü kaybı getirisi göz önünde alınmalıdır.

Uygulamasız Olmaz Diyenlere..

Yumuşatma ile ilgili uygulamaların çoğunun Low-Pass yani alçak geçiren bir filtre yapısında olduğunu söylemek sanırım yanlış olmaz. Günümüzde oldukça fazla yumuşatma algoritması mevcut olsa da (Additive, Savitzky–Golay, Ramer–Douglas–Peucker, Moving, Kalman..) ben bunların içinden mikrodenetleyiciye daha hızlı uyarlanması açısından üç tanesini seçtim; moving, laplace, triangular. FIR filtre yapısında olan bu algoritmaları kısaca belirtmek gerekirse;

1) Moving Averager: Moving averager yani hareketli ortalama belirli sayıda örneği alıp, basit bir FIFO yapısıyla filtrenin boyutuna göre ortalama almaktadır. Özellikle borsada çok fazla kullanılan filtrenin matematiksel ifadesini boyutu 3 olmak üzere aşağıda görebilirsiniz.

2) Laplace Averager: Hareketli ortalamadan farklı olarak Laplave Averager filtre yapısını bir FIFO tarzında kullanmaz. Örneğin filtre boyutu 10 olan bir laplace ortalama filtresi, öncelikle ilk 10 datayı toplar ve bunu 10’a bölerek ilk filtrelenmiş elemanı elde eder. Daha sonraki 10 örnek bekleme anında ise önceki filtrelenmiş değer sabit kalır. Bu bize gerçek sinyali takip etmeme gibi zorluk çıkarsa da basitlik açısından diğerlerinden avantajlıdır.

3) Triangular Averager: Üçgensel ortalama da ise aynen hareketli ortalamadaki FIFO mantığı kullanılır. Yalnız hareketli ortalamadan farklı olarak üçgensel ortalamada ölçülen değerler filtre boyutuna göre üçgen form oluşturacak katsayılar ile çarpılır ve bu katsayıların toplamına bölünür. Aşağıda 5 boyutlu üçgensel filtre için matematiksel ifade gözükmektedir.

Yukarıdaki üç filtrenin başarısı, filtre boyutu ile orantılı işlem süresi kısalığı ve küçük filtre boyutunda iyi bir filtreleme işlemi gerçekleştirmesine bağlıdır.

Örnek olarak sistemimizde okumak istediğimiz sinyal 1,5V offsetli 3Vpp genliğe sahip 50Hz sinüs sinyali olsun. Bu sinyalin üstüne ise random gürültü bindirelim.

Uygulamada 32-128 ve 2048 olmak üzere 3 filtre boyutu seçelim ve tüm filtrelerde aynı boyutları kullanalım. Kırmızılar ölçmek istediğimiz sinyali, maviler ise filtre çıkışlarını göstermektedir.

a) 32 Birim Uzunluğunda Filtre Sonuçları

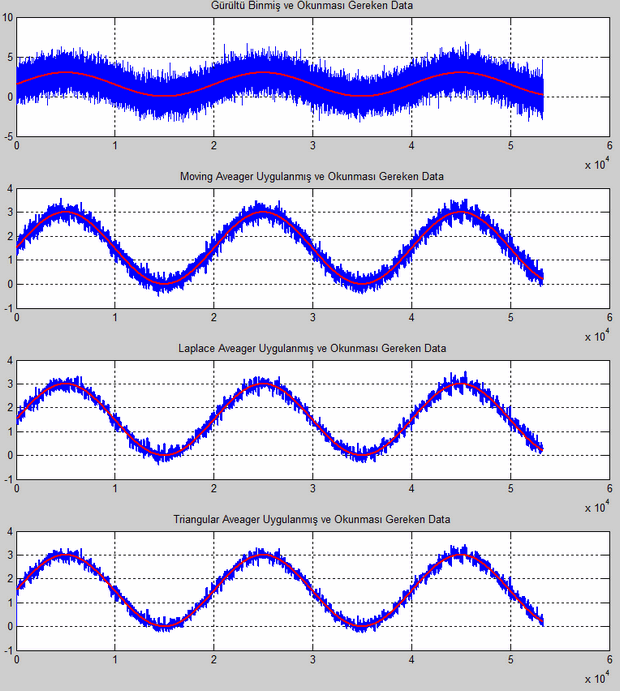
b) 128 Birim Uzunluğunda Filtre Sonuçları

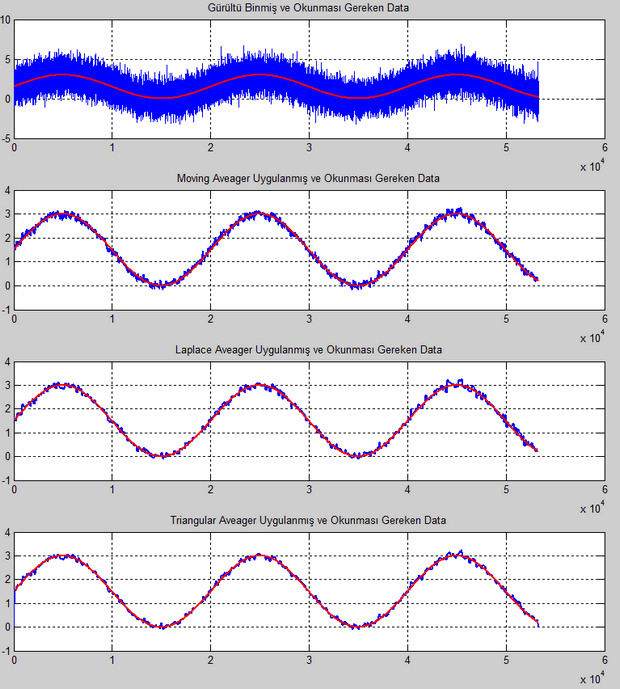
c) 2048 Birim Uzunluğunda Filtre Sonuçları

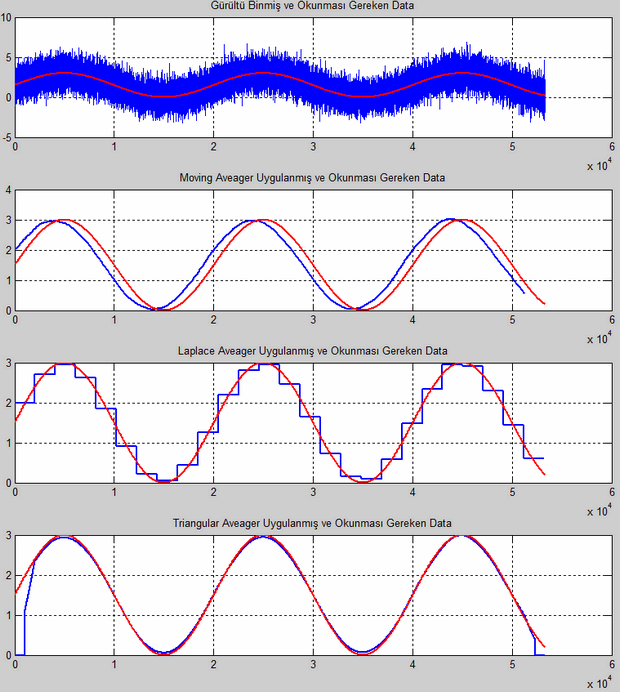
Sonuç Olarak..

Filtre boyutu ve gürültü bastırma oranları göz önüne alındığında triangle averager’ın diğerlerine nazaran daha iyi bir iş çıkardığı yukarıdaki resimlerden gözlemlenebilir. Filtre boyutu büyüdükçe hem moving hem de triangle averager çıkışları, ölçmek istediğimiz sinyale yaklaşmaktadır. Laplace averager ise boyut büyüdükçe basamaklı bir yapı haline gelmekte ve bizim okumak istediğimiz sinyalden uzaklaşmaktadır. Her filre filtrenin boyutu kadar sisteme bir faz farkı da eklemektedir. Gerçek ortamda sistem tasarlanırken bu faz farkının sistemi etkileyip etkilemediği incelenmeli ve buna göre filtre tasarlanmalıdır.

Herkese çalışmalarında başarılar dilerim..

Dip Not: Dijital filtre tasarlarken öncelikle sistemi z-domain’ine aktarıp, orada katsayılar bulunduktan sonra sistemin frekans cevabına bakılmalıdır. Ayrıca hangi frekansın ne kadar bastırıldığını incelemek için sinyal FFT ile açılmalı ve frekans bileşenleri ayrı ayrı incelenmelidir. Ben burada pratik açıdan sistemi incelediğim için tüm bunları göz ardı ettim.

Yaptığım uygulama ile ilgili MATLAB Dosyaları;