Lojik Devre Laboratuarı Deneyleri

Lojik Devre Laboratuarı Deneyleri Teorik detayları ile bir çok deney bulunmakta analog dijital çeviriciler, formüller, dijital kapılar ve daha bir çok bilgi bulunuyor ayrıca uygulama devrelerinede yer verilmiş. Emeği geçen Kişilere Teşekkürler.

TEMEL KAPI DEVRELERİ

Temel kapı devrelerinin işlemlerini ve bu işlemleri gerçekleştiren kapı devrelerinin incelenmesi ve gerçekleştirilmesi.

Dijital elektronik sistemler temel mantık kurallarına uygun çalışan sistemlerdir. Bu tür sistemlerde giriş ve çıkış , 0 ve 1 olmak üzere sadece iki duruma sahiptir. Bu durumdaki sayı sistemine ikili sayı sistemi denir. Mantık devreleri bu sayı sistemini kullanır. Temel olarak veya , and ve not olmak üzere üç tane lojik kapı devresi mevcuttur.

Temel lojik kapı devreleri diyot ve transistorlerle kurulan çeşitli devrelerle oluşturulurlar. Sayısal elektronik uygulamalarında transistör kullanılırken transistorün kesim ve doyum çalışma bölgelerinden faydalanılır. Bir transistorün base akımı sıfır olduğunda , o transistör kesimdedir. Base akımı belli bir değere ulaştığında transistör doyum durumuna geçer. Kesimde olan bir transistorde kollektör- emiter arası açık devre , doyumda ise kısa devre gibi davranır. Bu çalışma durumuna transistorün anahtarlama çalışma durumu denir.

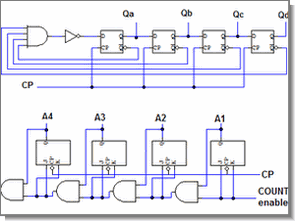
VEYA kapısı , girişlerin hepsi sıfır olduğunda sıfır çıkış üreten , en az bir girişi lojik 1 olduğunda lojik 1 çıkışı üreten bir devredir. Şekil-1’de diyotlarla oluşturulan iki girişli bir VEYA kapısı görülmektedir. Bu devrede her iki girişi de lojik 0 uygulandığında D1 ve D2 diyotlarının her ikisi de kesim durumundadır. Diyotların her ikisi de kesim durumunda olduğunda veya kapı devresi çıkışı F lojik 0 değerine sahiptir. Girişlerden en a birine lojik 1 uygulandığında (+5V) ilgili diyot doğru yönde polarlanarak girişteki lojik 1 seviyesi F çıkış noktasına aktarılır.

Şekil 1: Diyot İle VEYA Kapı Devresi

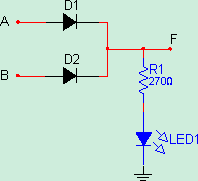
Şekil-2’de transistorlerden oluşan iki girişe sahip bir VEYA kapıdevresi görülmektedir. Bu devrede girişlerden her ikisi de lojik 0 olduğunda transistorler kesim durumundadır. Bunun anlamı her iki transistorün de kesim durumunda olmalarından dolayı R direnci üzerinden herhangi bir akım geçmeyecek ve F çıkışı lojik 0 durumunda kalacaktır. Girişlerden en az bir tanesi lojik 1 olduğunda ilgili transistor iletim durumuna geçer. Bu durumda transistorun Ic akımı R direnci üzerinden devresini tamamlayarak F çıkışı üzerinde bir gerilim düşümüne sebep olur. Bu F çıkışı lojik 1 değerindedir.

Şekil 2: Transistorlü VEYA Kapısı

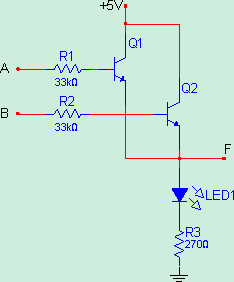
Şekil-3’de diyotlu VE kapısı görülmektedir. Bu devrede her iki giriş de lojik 0 olduğunda diyotların her ikisi de doğru yönde polarlanacağından dolayı F çıkışında sadece 0.6V görülecektir.bu potansiyel farkı lojik 0 olarak değerlendirilir. Girişlerden bir tanesi lojik 0 , diğeri lojik 1 seviyesinde olduğunda durum değişmeyecektir. Çünkü bu durumda diyotlardan bir tanesi iletim , diğeri ise kesimdedir. İletim durumundaki diyotun girişi lojik 0 olduğundan dolayı F çıkışı bu diyot üzerinden şaseye bağlandığı için lojik 0 seviyesinde olacaktır.bu devrede her iki giriş lojik 1 seviyesinde olduğunda , diyotlar ters polarlanmış olacak ve besleme gerilimi F çıkışında görülecektir. Bu çıkış ise lojik 1 olarak değerlendirilir.

Şekil 3: Diyotlu VE Kapısı

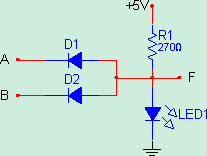
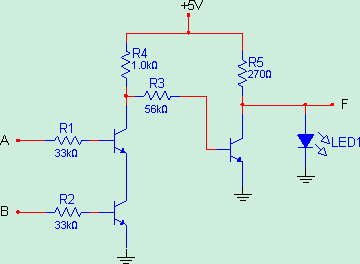
Şekil-4’teki devrede girişlerin her ikisi de lojik 1 seviyesinde olduğunda , transistorlerin her ikisi de iletim durumunda olacak ve A noktası şaseye bağlanmış olacaktır. Bu durumda ise F ucuna bağlı olan transistor kesim durumuna geçecek ve F çıkışı lojik 1 seviyesine geçecektir.

Şekil 4: Transistorlü VE kapısı

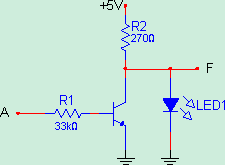
Girişe uygulanan lojik 0 işaretini çıkışına lojik 1 , lojik 1 işaretini ise lojik 0 olarak çıkışa aktaran devrelere DEĞİL kapısı denir. Şekil-5’de ise bir DEĞİL kapısının transistorlerle gerçekleştirilmiş devresi görülmektedir.

Şekil 5: Transistorlu DEĞİL kapısı

DENEYİN YAPILIŞI

1. Şekil-1 ve Şekil-2’deki VEYA kapı devrelerini kurarak , doğruluk tablolarını çiziniz.
2. Şekil-3 ve Şekil-4’teki VE kapı devrelerini kurarak , doğruluk tablolarını çiziniz.
3. Şekil-5’teki DEĞİL kapı devresini kurarak , doğruluk tablosunu çıkarınız.

SONUÇ

Şekil-1 ve şekil-2’de girişlerin en az birine lojik 1 uygulandığında çıkışta 5V gözleyeceğiz. Girişlerin her ikisine de lojik 0 uygulandığında çıkışta 0 volt gözükecektir.

Şekil-3 ve şekil-4’te en az birine lojik 0 uygulandığında çıkışta 0 volt görülecektir. Girişlerin her ikisi de lojik 1 olduğunda çıkışta 5V görülür.

Şekil-5’teki devrede girişe lojik 0 uygulandığında çıkış lojik 1 , girişe lojik 1 uygulandığında ise çıkış lojik 0 olacaktır.

KOMBİNASYONEL LOJİK DEVRELER

MSI lojik elemanları yardımı ile kombinasyonel lojik devrelerden toplayıcı ve çıkarıcı devrelerinin kurulması ve incelenmesi.

Sayısal bilgisayarların gerçekleştirilebildikleri bir çok bilgi işleme şekillerinden birisi de aritmetik işlemlerdir. En temel aritmetik işlem , iki binary dijitin toplanmasıdır. Bu basit toplama işlemi dört farklı işlemden oluşur.

0+0=0 , 0+1=1 , 1+0=0 , 1+1=1 işlemlerinden ilk üç işlemde toplamın boyutu bir dijit oluşmasına rağmen , dördüncü işlemde toplayan ve toplanan binary bilgilerin her ikisinin de 1 olması durumunda işlem sonucunda elde edilen toplamın boyutu iki dijittir. Bu durumda elde edilen sonucun en ağırlıklı biti elde olarak adlandırılır. İki bit bilginin toplamını gerçekleştiren kombinasyonel devrelere yarı toplayıcı , üç bit bilginin toplamını gerçekleştiren devrelere de tam toplayıcı denir.

Şekil 1:Yarım Toplayıcı

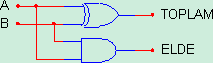
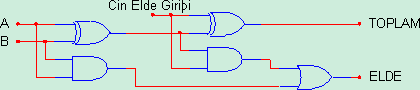
Şekil-1’deki devre yarım toplayıcıdır. Şekil-2’den de görüldüğü üzere bir tam toplayıcı , iki yarım toplayıcı ve bir OR kapısından oluşmaktadır. Şekil-2’deki tam toplayıcı iki adet bir bitlik bilgilerin toplanmasını gerçekleştirmektedir. Eğer toplanacak bilgiler bir bitten büyük olursa , bit sayısı kadar tam toplayıcı paralel olarak kullanılacaktır. Her tam toplayıcının elde çıkışı kendinden sonra gelen tam toplayıcının elde girişine uygulanır.

Şekil 2:Tam Toplayıcı

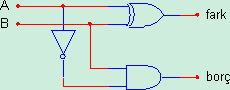
Toplama işleminde olduğu gibi çıkarma işleminde de 0-0=0 , 0-1=1 , 1-0=1 ve 1-1=10 olmak üzere dört temel işlem bulunmaktadır. Bu işlemleri gerçekleştiren kombinasyonel devrelere yarım çıkartıcı denir. Çıkartma devreleri toplama devresine benzer. Toplayıcı devredeki toplam çıkışı bir fark çıkışı ile ve elde çıkışı bir borç çıkışı ile yer değiştirirse yarım çıkarıcı devresi elde edilir. Yarım toplayıcı da elde çıkışı yerine yarım çıkarıcı devrede borç çıkışı vardır. 0’dan 1 çıkarılırken , bir sonraki bitten bir borç alınır ve 10 ikili bilgisinden 1 çıkartılır. Şekil-3’te bir yarım çıkarıcı devresi verilmiştir.

Şekil 3:Yarım çıkarıcı

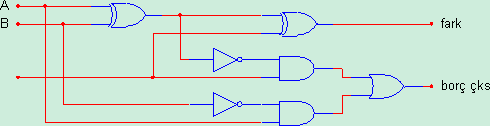
Bir tam çıkarıcı ise iki yarım çıkarıcı ve bir OR kapısından oluşmaktadır. Bu devre şekil-4’de görülmektedir.

Şekil 4:Tam çıkarıcı

Şekil-5’te 4 bitlik tam toplayıcı , şekil-6’da ise toplam sonucunu BCD’ye çevirebilen 4 bitlik bir tam toplayıcı devresi görülmektedir.

DENEYİN YAPILIŞI

1. Şekil-1’deki devreyi kurunuz ve çalışmasını inceleyiniz.
2. Şekil-2’deki devreyi kurunuz ve çalışmasını inceleyiniz.
3. 74LS83 IC paketi yardımıyla 4 bitlik paralel toplayıcı yapınız.
4. Şekil-3’deki devreyi kurunuz ve çalışmasını inceleyiniz.
5. Şekil-4’deki devreyi kurunuz ve çalışmasını inceleyiniz.
6. Şekil-5’teki devreyi kurunuz ve 4 bitlik toplama çıkarma örnekleri yapınız.

Şekil 5: 4 bit tam toplayıcı

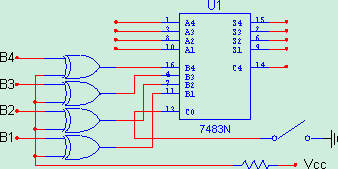
7. Şekil-6’daki devreyi kurunuz ve 4 bitlik BCD çevrimli toplama , çıkarma örnekleri yapınız.

Şekil 6: BCD çevrimli 4 bit tam toplayıcı

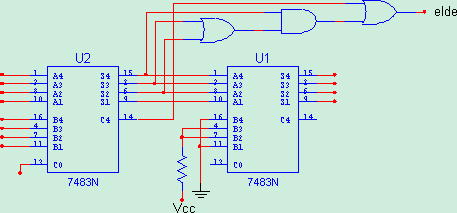
SONUÇ

Şekil-2’deki devrede A,B ve Cin girişleri var. Devreden Tablo-2 ‘deki sonuçları alırız.

Tablo 1

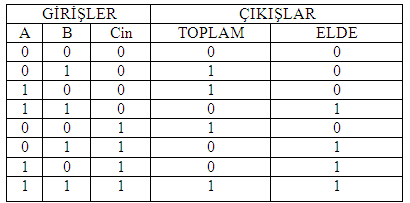
Şekil-4’deki devrede aşağıdaki sonuçlar bulunur.

Tablo 2

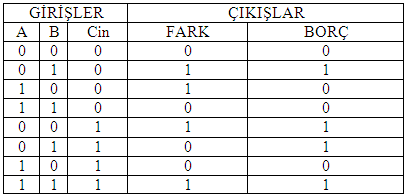
Ardışık devrelerden olan SAYICI devrelerinin kurulması ve çalışma esaslarının incelenmesi.

Girişine clock palslarının uygulanması ile durumunu , önceden bilinen bir sıra dahilinde değiştiren ardışık devrelere sayıcı (counter) denir. Sayma palsları olarak bilinen giriş palsları bir clock palsı üretecinden sağlanabileceği gibi , harici başka bir kaynaktan belirli zaman aralılarında ya da rasgele de sağlanabilir. Sayıcılar genellikle belirli bir olayın kaç kere oluştuğunun sayılmasında ve dijital sistemlerde işlemlerin kontrol edilmesi için gerekli olan zamanlamanın elde edilmesinde kullanılırlar.

Binary bir sırayı takip eden bir sayıcı ; binary sayıcı olarak da adlandırılır ve n- bitlik bir binary sayıcı n adet flip-flop’tan oluşur. n- bitlik bir binary sayıcı , binary formda 0(sıfır) dan 2N-1’e kadar sayar. MSI sayıcılar genel olarak iki gurupta ele alınabilirler. Bunlar ; RIPPLE sayıcılar ve SENKRON sayıcılardır.

Temel hafıza paketleri kullanılarak yapılan hafıza organizasyonu ve bilgi kaydı işlemlerinin incelenmesi ve devrelerin gerçekleştirilmesi. Günümüzde kullanılan en küçük mikroişlemci sisteminden en büyük bilgisayar sistemine kadar bütün bilgisayar sistemleri kullandıkları programları ve bilgileri depolayabilmek için binlerce bitik hafıza birimlerine ihtiyaç duyarlar. Bu ihtiyacın karşılanabilmesi için birçok depolama birimi geliştirilmiş ve kullanıma sunulmuştur. Yarı iletken hafızalar da bunlardan biridir.

DENEY 1 TEMEL KAPI DEVRELERİ
DENEY 2 KOMBİNASYONEL LOJİK DEVRELER-1
DENEY 3 KOMBİNASYONEL LOJİK DEVRELER-2
DENEY 4 ARDIŞIK LOJİK DEVRELER-1
DENEY 5 ARDIŞIK LOJİK DEVRELER-2
DENEY 6 SAYICILAR-1
DENEY 7 SAYICILAR-2
DENEY 8 HAFIZALAR
DENEY 9 ARİTMETİK VE LOJİK İŞLEM BİRİMİ (ALU)
DENEY 10 ANALOG-DİJİTAL VE DİJİTAL-ANALOG ÇEVİRİCİLER