Fourier dönüşümü hakkında bilgiler

Picproje forumlarında “mihri” isimli kullanıcı “Fourier dönüşümü hakkında” faydalı bir doküman hazırlamış formuller ve grafiksel olarak anlatım yapılmış aşağıda ilk bölüm bulunuyor

1.0 Fourier Kimdir?

Bu sorunun cevabını merak edenler (http://tr.wikipedia.org/wiki/Fourier) linke tıklayarak bilgi edinebilirler. Bizim asıl amacımız Fourier kardeşimizin ortaya attığı teoriyi kavrayabilmek ve uygulamalarımızda kullanabilecek düzeyde bilgi edinmek olduğu için ben direkt konuya dalmak istiyorum.

1.1 Fourier’in ortaya attığı teorem;

Fourier’ in teoremine göre doğadaki tüm periyodik fonksiyonlar, birbirine dik iki farklı periyodik fonksiyonun artan frekanslardaki değerlerinin dik toplamı şeklinde gösterilebilir. Fourier bu toplamı sinüs ve kosinüs fonksiyonlarını kullanarak göstermiştir.

1.2 Fourier serisi;

Günümüzde Euler bağıntısı kullanılarak sinüs ve kosinüs fonksiyonları yerine karmaşık üslü sayılar kullanılmaktadır. Fonksiyonların karmaşık üslü sayıların toplamı olarak gösterilmesine Fourier serisi gösterimi denir.

1.3 Fourier serisi ne işe yarar?

Fourier açılımı sayesinde fonksiyonların frekansı kolaylıkla belirlenebilir. Bu yaklaşım farklı
periyotlarda girdiye maruz kalan sistemlerin çıktısını ve çıktısının frekansını belirlemekte
kolaylık sağlar.

Bu son paragrafı biraz daha açarsak konunun daha iyi anlaşılacağını zannediyorum. Mesela
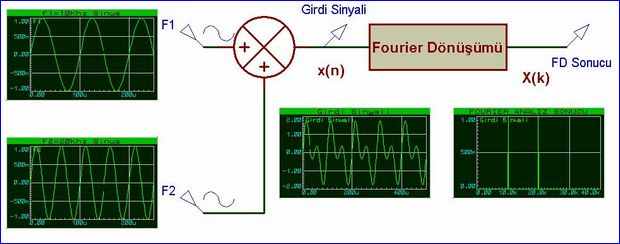
girdisi iki farklı fonksiyondan oluşan Fourier analizinin nasıl bir sonuç vereceğini inceleyelim.

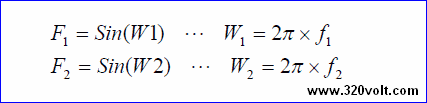
F1 Fonksiyonunun frekansı 10Khz ve F2 fonksiyonunun frekansı 20Khz olsun Şekil 1.3.1’de gösterilen Fourier analizi sonucu grafiği görülmektedir. Grafiğe göre girdi sinyali genlikleri 1 olan 2 adet sinüs fonksiyonunun toplamına eşittir ve giriş sinyallerinin frekansları sırası ile 10Khz ve 20Khz’dir. Gerçektende girişte uygulanan sinyaller 10Khz ve 20Khz frekanslı sinüs fonksiyonlarıdır.

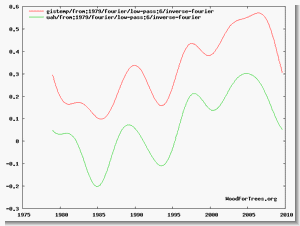
Şimdi de Fourier teoreminin temeline bir örnek verelim. Konu 1.1’de verilen bilgiye göre doğada bulunan periyodik her işaret sinüs ve kosinüs fonksiyonlarının toplamı şeklinde gösterilebilir, öyleyse 1Khz kare dalga sinüs ve kosinüs fonksiyonlarının toplamı şeklinde yazılabilmelidir. Kare dalganın Fourier dönüşümünü alırsak aşağıdaki matematiksel fonksiyonu elde ederiz.

Denklem 1.3.1

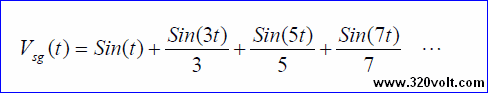
Kosinüslü terimlerin katsayıları 0 olduğu için bu fonksiyonlar gösterilmemiştir.

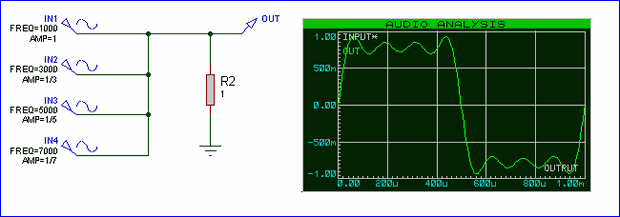
Şekil 1.3.2 de görüldüğü gibi Fourier serilerinden elde edilen sinyal yaklaşık kare dalga şeklinde. Biz sadece genliği 0’dan farklı ilk 4 harmoniği kullandığımız için tam kare dalga elde edemedik. Seride yer alan harmonik sayısı arttıkça elde edilen sinyal kare dalgaya daha fazla yaklaşacaktır. Sonsuz seri tam kare dalga demek, zaten Fourier dönüşüm denklemi bunu işaret ediyor. Artık temelde Fourier dönüşümünün ne olduğunu anladıysak işi birazda formüllere dökelim.

Denklem 1.3.2 Sürekli zaman Fourier dönüşümü.

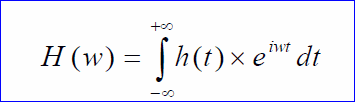
Denklem 1.3.3 Ters Fourier dönüşümü.

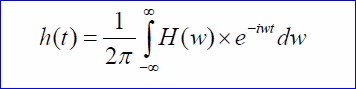
Sürekli zaman denklemleri ile fazla zaman kaybetmeyeceğiz çünkü sonsuz frekans sonsuz genlik… ifadeleri matematikçileri ilgilendiren ifadelerdir. Gerçek dünyada bu ifadelerin mümkün olmadığını hepimiz biliyoruz.  Mühendisin ilgi alanı da gerçek dünya olduğuna göre ayrık Fourier dönüşümü (AFD) üzerine yoğunlaşmamız daha doğru olacaktır. Mikro denetleyicilerde koşturulan HFT (FFT) algoritmalarda aslında AFD (DFT) algoritmalarının optimize edilerek daha hızlı sonuç veren halidir. Bir sonraki yazıda AFD (ayrık Fourier dönüşümü) hakkında bilgi vermeye çalışacağım. Şimdilik hoşça kalın.

devamını (gelirse) kaynak konu üzerinden takip edebilirsiniz. Emeği geçen hazırlayan kişilere teşekkürler