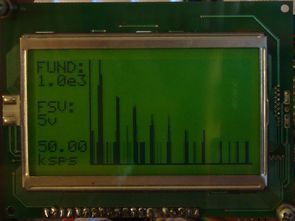
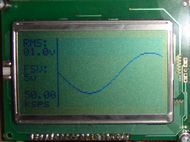
Circuit dspic30f4011 microcontroller with 128 x 64 graphic lcd ACD used the information in the MCP6S21 (Lumex LCM-S12864GSF) on the display. All project source code, schematics have also given the detail description..
Facing the demise of my Tektronix 2213 in an unfortunate shipping journey, I faced the decision of either purchasing an expensive CRT to get it running again, or spending my nights surfing ebay for another scope.
The oscilloscope consists of an input stage consisting of a resistive attenuator with 1Mohm impedance, a switch to remove or insert a capacitor for AC or DC coupling, followed by several amplifiers. The first amplifier is a unity gain inverting buffer, followed by a level shifting circuit to center the signal around .5Vcc (2.5V) for the PGA and ADC. The stage immediately preceding the ADC pin on the dsPIC is a Microchip MCP6S21 PGA



Source: http://www.circuitcellar.com
FILE DOWNLOAD LINK LIST (in TXT format): LINKS-14184.zip
Published: 2011/03/15 Tags: dspic projects, microchip projects, microcontroller projects
Fast Fourier transformation FFT Circuit ATmega8 SCT2024 LED driver
ATmega8 (TQFP32 package) based on FFT Circuit applied the entry signals 16 × 16 led display (SCT2024 serial-interfaced LED driver 256 LEDs), you can see in the FFT circuit source C, hex codes have a parent/child schema for the printed circuit drawings a good example about the use of the SPI, ADC with atmega8
Fast Fourier transformation
A fast Fourier transform (FFT) is an algorithm to compute the discrete Fourier transform (DFT) and its inverse. Fourier analysis converts time (or space) to frequency and vice versa; an FFT rapidly computes such transformations by factorizing the DFT matrix into a product of sparse (mostly zero) factors. As a result, fast Fourier transforms are widely used for many applications in engineering, science, and mathematics. The basic ideas were popularized in 1965, but some FFTs had been previously known as early as 1805. Fast Fourier transforms have been described as “the most important numerical algorithm of our lifetime”.